В длинном коридоре есть сто дверей, подписанных номерами, изначально все двери закрыты. Программист проходит мимо дверей, меняя их состояние: закрытые открывает, а открытые — закрывает. В первый обход он касается всех дверей, чей номер кратен единице, во второй — чей номер кратен двум, в третий — трём, в четвёртый — четырём. Всего программист делает сто таких обходов. Если что, кратен — это значит, что номер двери делится на это число без остатка.
Какие двери останутся открытыми после сотого обхода?
Представим нашу задачу визуально. До первого обхода программиста все сто дверей закрыты:

В первый обход программист меняет состояние каждой двери, то есть открывает их:

Во второй обход он закрывает все двери с номером, кратным двум, то есть каждую вторую: 2, 4, 6, 8, 10, 12 и так далее.

В третий обход он закрывает или открывает все двери с номером, кратным трём, — каждую третью: 3, 6, 9, 12, 15, 18 и так далее.

Попробуем порассуждать и для примера возьмём дверь с номером 50. Поскольку число 50 кратно числам 1, 2, 5, 10, 25 и 50, получается, что программист коснётся этой двери в первый, второй, пятый, десятый, двадцать пятый и пятидесятый обходы. Вот как будет меняться состояние двери:
- Открыто (первый обход, когда программист коснётся всех дверей с номером, кратным 1).
- Закрыто (второй обход, когда программист коснётся всех дверей с номером, кратным 2).
- Открыто (пятый обход, когда программист коснётся всех дверей с номером, кратным 5).
- Закрыто (десятый обход, когда программист коснётся всех дверей с номером, кратным 10).
- Открыто (двадцать пятый обход, когда программист коснётся всех дверей с номером, кратным 25).
- Закрыто (пятидесятый обход, когда программист коснётся всех дверей с номером, кратным 50).
Получается, что двери, которых программист коснётся чётное число раз, после сотого обхода останутся закрытыми. А двери, которых программист коснётся нечётное число раз, останутся открытыми.
Проанализируем эту ситуацию и выведем закономерность. Дверь с номером 50 будет открыта и закрыта за шесть обходов:
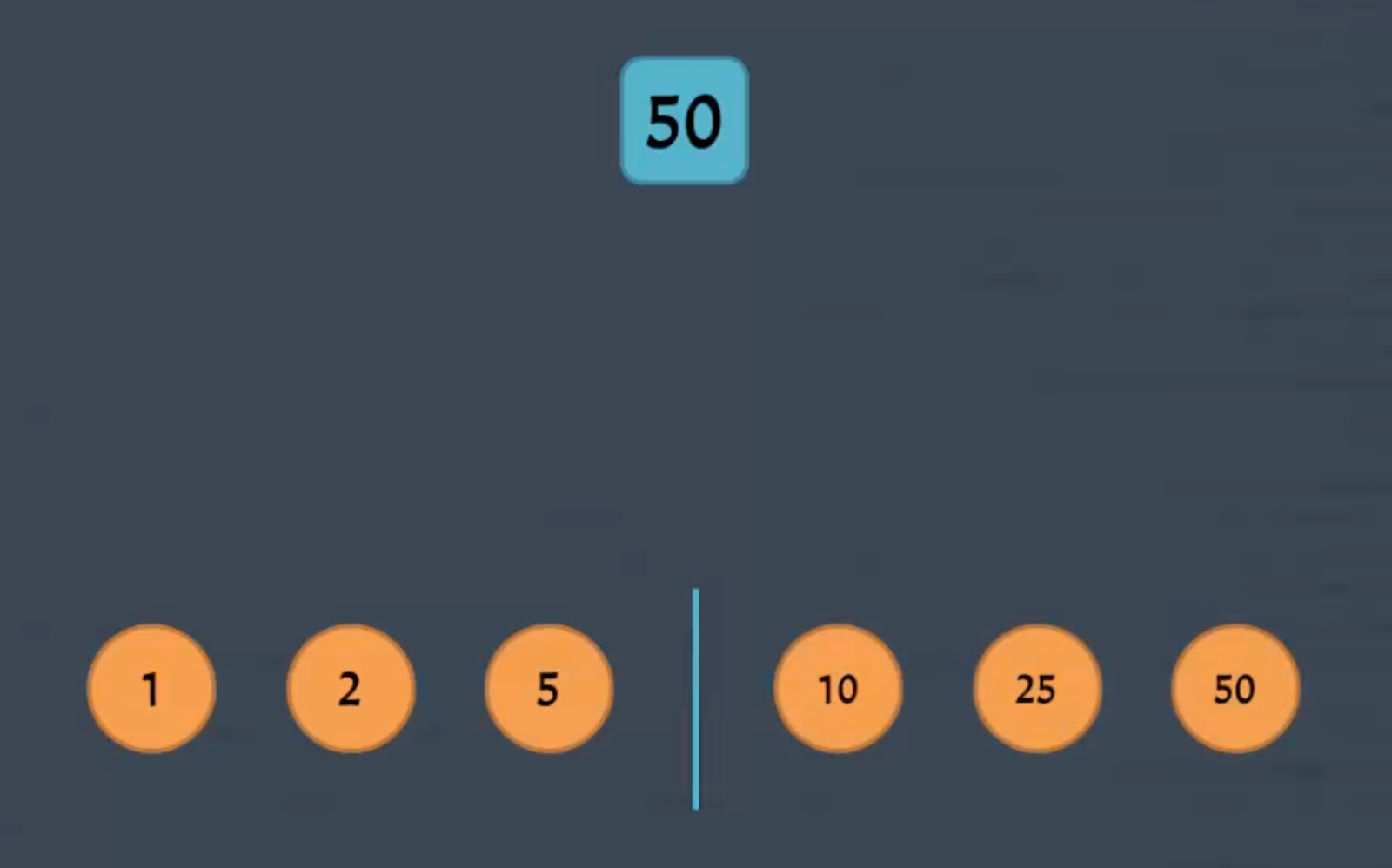
При умножении номеров первого и последнего, второго и предпоследнего и третьего и четвёртого обходов мы получим число номера двери — 50:
1 × 50 = 50
2 × 25 = 50
5 × 10 = 50
Похожей будет закономерность для всех дверей, которых программист коснётся чётное число раз. А какой она будет для остальных дверей?
Представим дверь с номером X, которой программист коснётся нечётное число раз, например пять:
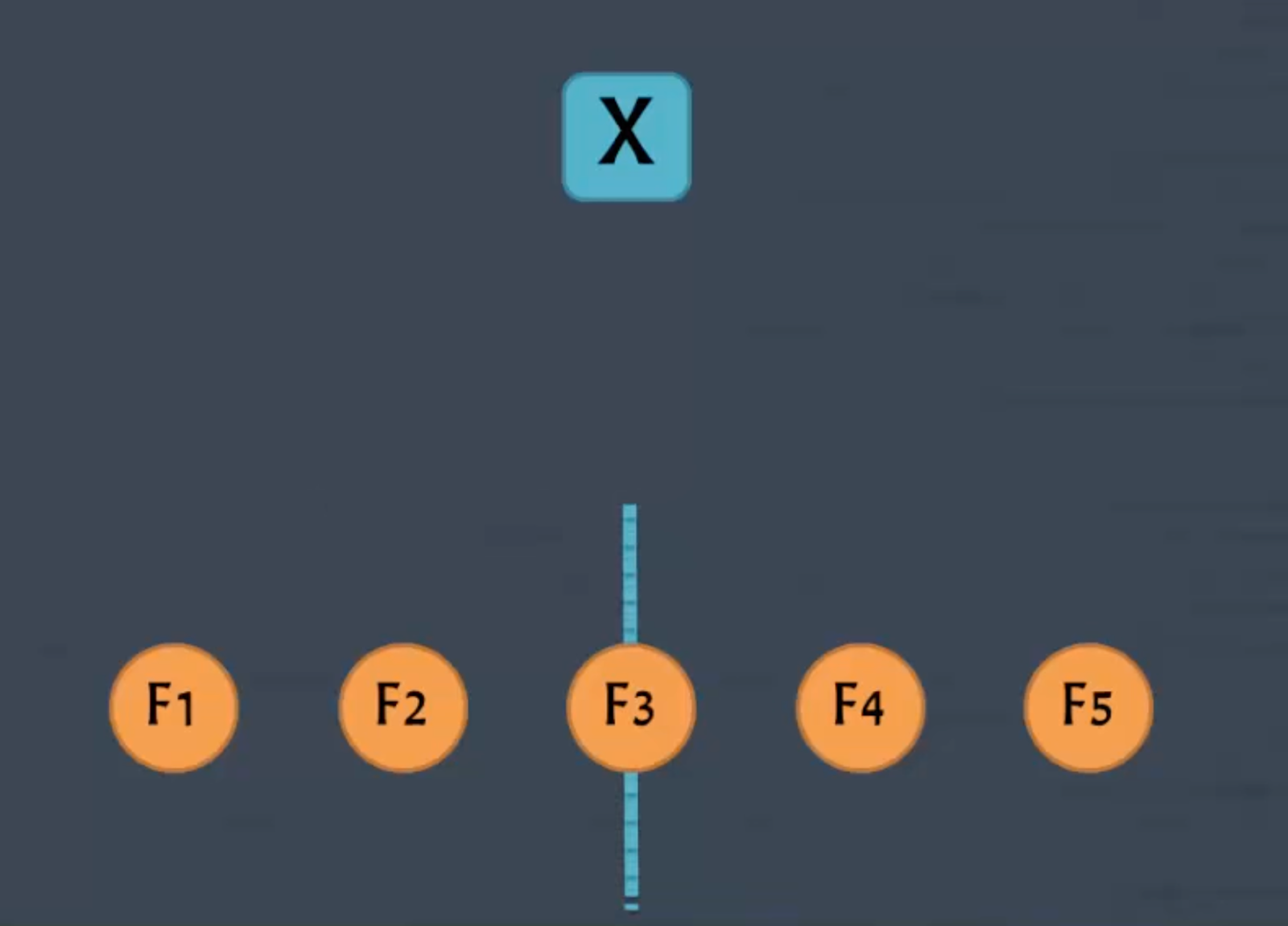
Получается, что для такой двери будут верны следующие уравнения:
F1 × F5 = X
F2 × F4 = X
F3 × F3 = X
Последнее уравнение получается квадратным:
F32 = X
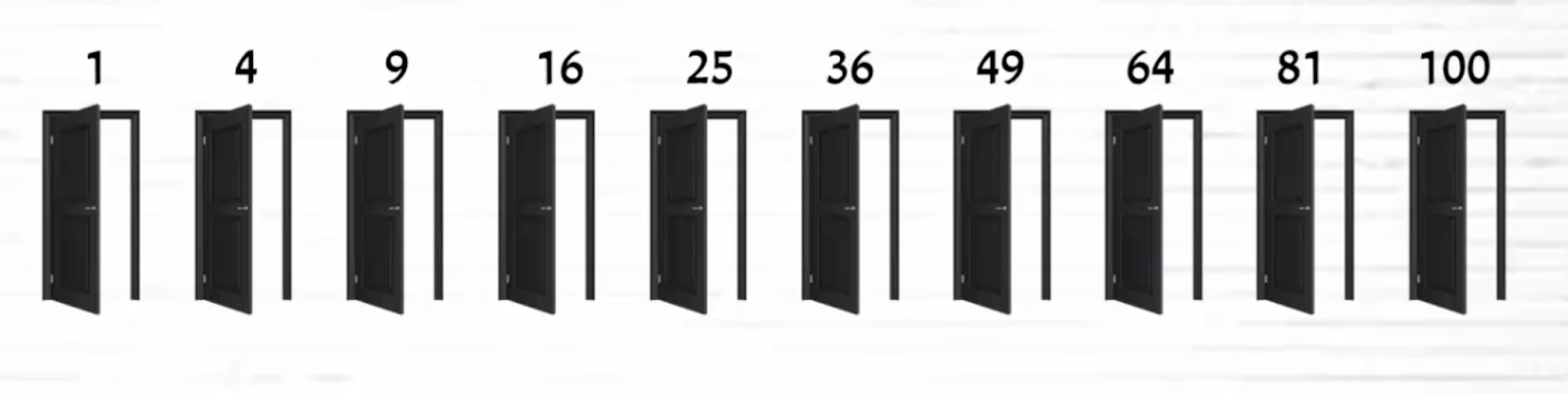
Из этого следует, что открытыми останутся двери, номера которых получаются из умножения номера обхода на него же:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100.
Для решения на Python нам нужно будет учесть два момента:
- Нумерация в списках идёт с нуля, поэтому для точного номера двери нам нужно будет прибавить к индексу единицу.
- Команда диапазона
range()не включает в себя правую границу, поэтому если написано range(100), то в диапазоне окажутся числа от 0 до 99. А если мы укажем два параметра — range(1,101), то в диапазоне будут числа от 1 (оно включается) до 100 (потому что 101 не включается).
Зная это, напишем простой код, который за нас пройдёт по 100 раз мимо всех дверей и откроет (1) и закроет их (0) по правилам из условия.
# создаём пустой список дверей
doors = []
# теперь создаём сто новых дверей
for i in range(100):
# и делаем все их закрытыми
doors.append(0)
# делаем 100 проходов
for i in range(1,101):
# и в каждом проходе смотрим все двери
for j in range(100):
# если номер двери нацело делится на номер прохода
if (j+1) % i == 0:
# если она закрыта
if doors[j] == 0:
# открываем её
doors[j] = 1
# а если открыта
else:
# то закрываем
doors[j] = 0
# смотрим в итоге все двери, в каком они состоянии
for i in range(100):
# если очередная дверь открыта
if doors[i] == 1:
# то выводим её номер
print(i+1)















