Помните, когда мы в школе проходили все эти синусы, косинусы и углы, у всех был вопрос — а как нам это пригодится в жизни? Тогда казалось, что это нужно только учёным и математикам, но на самом деле всё трёхмерное моделирование и 3D-игры — это та самая школьная тригонометрия.
При чём тут 3D
В одной из статей мы рассказывали про 3D-игру Doom. Одной из особенностей этой игры было то, что у неё не было настоящей трёхмерной графики — движок оперировал двумерными моделями. Но на экране казалось, что это настоящая трёхмерность:
- можно было понять, что находится ближе, а что — дальше;
- если подойти к двери, она увеличивалась, а если отойти — уменьшалась;
- когда враги приближались, они становились больше, а на горизонте их было почти не видно и так далее.
Всё дело — в угле зрения. От него зависит, каким будет казаться объект, маленьким или большим, и как он изменит свой размер на разных расстояниях.
Угол зрения
Чтобы понять, что такое угол зрения, нам нужно знать всего две величины — высоту объекта и расстояние до него:
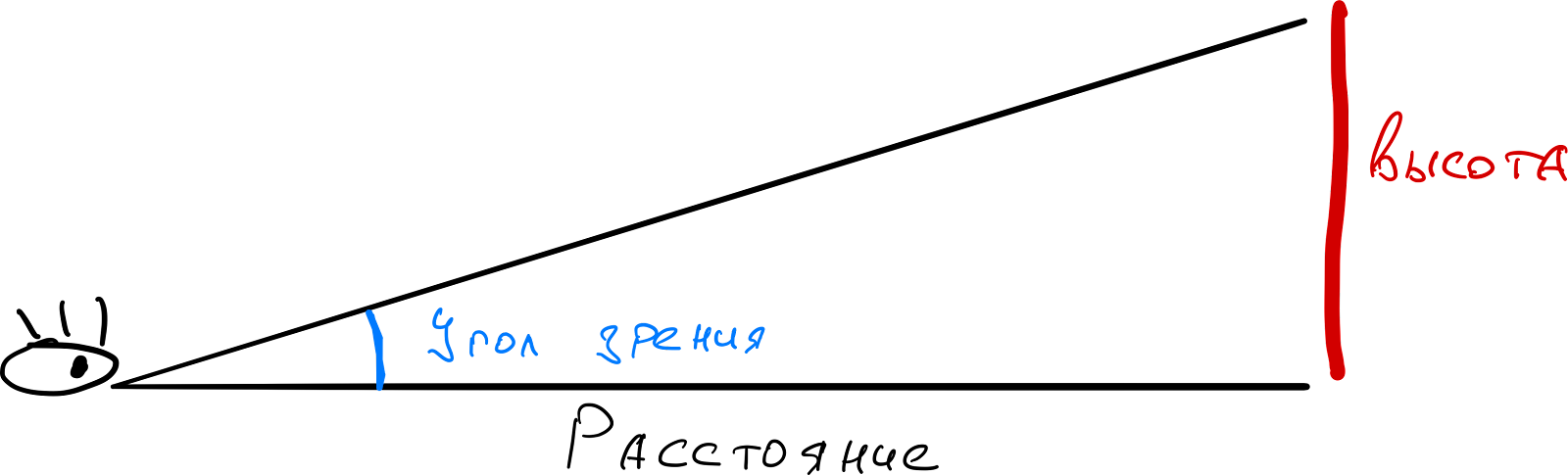
Сейчас наблюдателю наш красный объект кажется далёким, потому что угол зрения — маленький. Но если мы подвинем этот объект поближе к наблюдателю, то угол зрения станет больше:
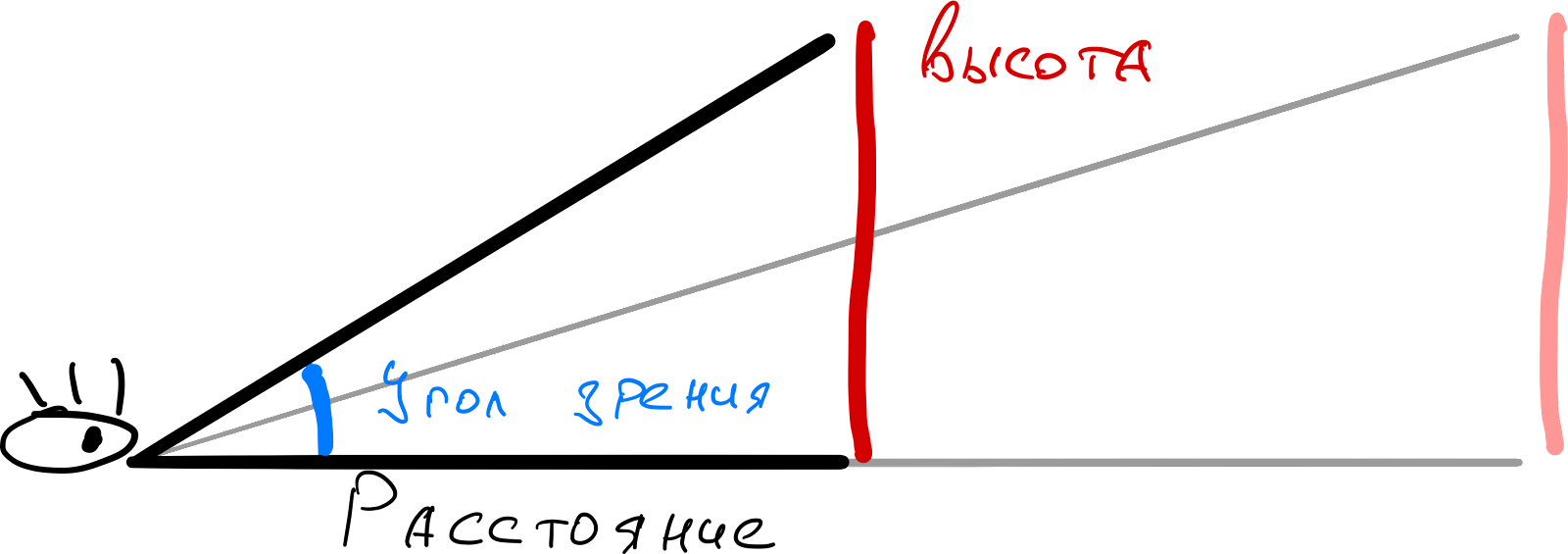
Теперь наблюдателю кажется, что объект очень близко, потому что угол зрения стал гораздо больше, чем раньше. Получается, что угол зрения влияет на то, как мы воспринимаем предметы — близкими или далёкими.
И вот тут нам пригождается школьная тригонометрия — все эти синусы, косинусы и тангенсы. Благодаря им мы сможем рассчитывать нужный размер предметов на экране в зависимости от того, какой угол получится между нашей виртуальной камерой и разницей в высоте предмета. Это позволит нам смоделировать разное расстояние до предметов, как будто у двумерного плоского экрана появляется третье измерение — глубина.
Как писали игры для приставок: чудеса оптимизации и жёсткий кодинг
Что такое обратная совместимость
Что такое эмулятор
Квадратный корень, который ускорил игры в сто раз
Новые чудеса оптимизации: как делали игру «Принц Персии»
Что такое виртуализация
4 виртуальные машины на любой случай
Что такое образ дискаНенастоящее 3D в DOOM
Из школьной программы мы помним формулу тангенса:
tg α = высота / расстояние, где α — наш угол зрения.
Единственное, что отличает на экране далёкие предметы от близких, — это высота, поэтому мы можем регулировать её так:
высота = расстояние × tg α.
Если расстояние будет равно единице, то высота объекта — это просто будет тангенс угла зрения альфа.
А раз так, то мы можем это использовать для эффекта 3D:
- Берём любой объект
- Выясняем, какой будет угол зрения для этого объекта, если подойти к нему вплотную, насколько позволяет игровой движок.
- Теперь если нам нужно показать, что мы отходим от объекта, то мы просто уменьшаем угол зрения. С ним уменьшится и тангенс, и высота объекта на экране.
- То же самое и с приближением — чтобы показать на экране, что мы как будто подходим к объекту, мы просто увеличиваем угол зрения, а с ним увеличивается и высота. Кажется, что мы подошли поближе.
Как видите, тут нигде нет расстояния до объекта — только угол зрения, который создаёт эффект приближения или удаления. Чистая тригонометрия.
Настоящее 3D
В настоящем 3D синусы и косинусы нужны, чтобы посчитать новые координаты всех сторон движущегося объекта. Штука в том, что нам нужно перенести объёмный трёхмерный объект на плоский двумерный экран — сделать проекцию.
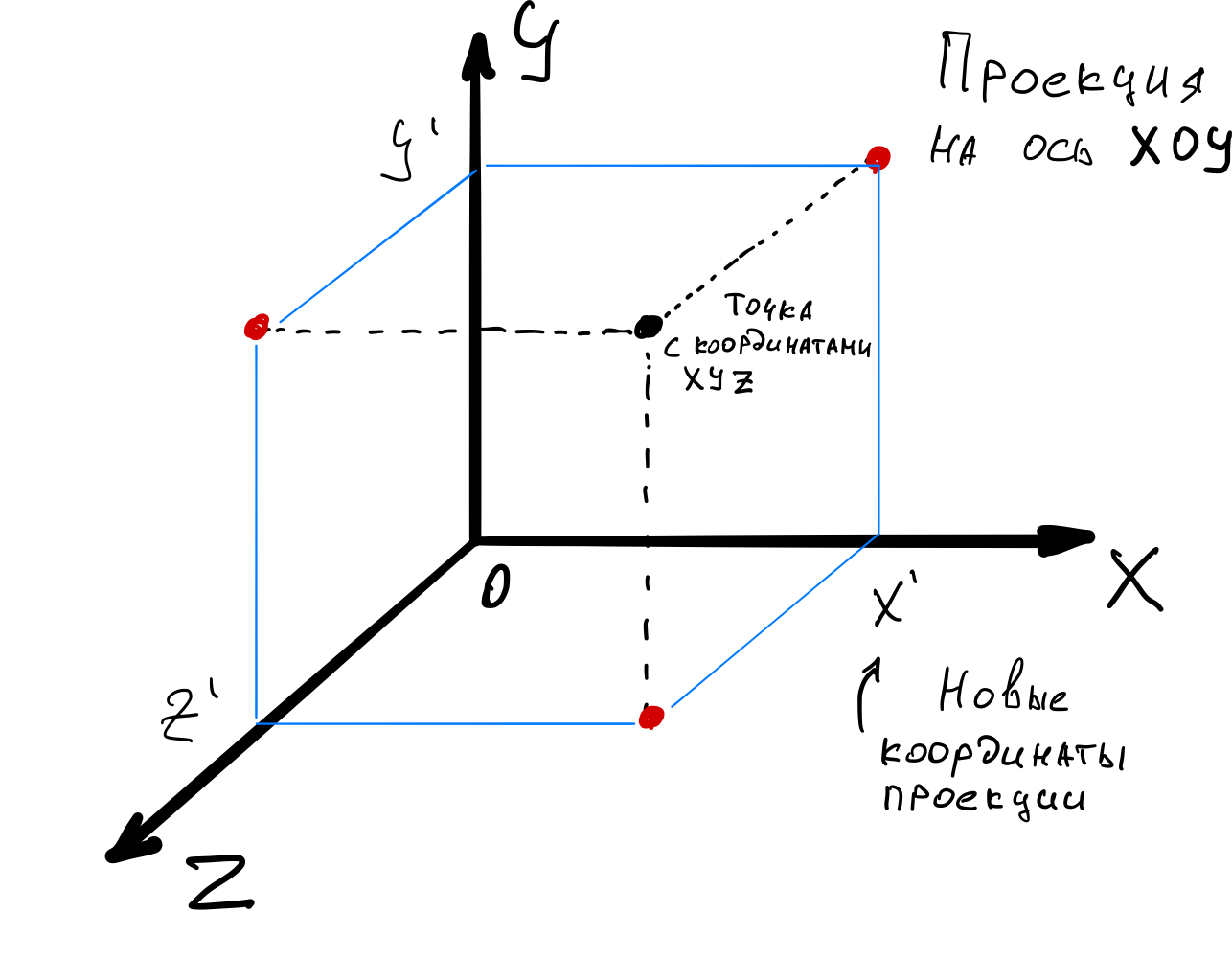
На плоской поверхности у нас есть только две координаты — X и Y, поэтому нам нужны формулы, которые помогут учесть третью координату Z и нарисовать объект так, чтобы он выглядел объёмным:
x’:=x*sin(угол между плоскостью XOY и отрезком OZ) ;
y’:=y*cos(угол между плоскостью XOY и отрезком OZ) ;
Чтобы трёхмерные объекты на экране можно было двигать, тоже используют тригонометрию. Например, если у нас есть трёхмерный кубик, у вершин которого есть координаты x, y и z, то, чтобы его повернуть на угол L по оси X, нужно сделать такое для каждой вершины:
x’=x;
y’:=y*cos(L)+z*sin(L) ;
z’:=-y*sin(L)+z*cos(L) ;
Здесь x’, y’ и z’ — новые координаты вершины. Если мы нарисуем кубик с такими новыми координатами каждой вершины, то будет казаться, что мы его немножко повернули.
Для других координат это работает похожим образом — нужно просто знать угол поворота для каждой оси, чтобы правильно посчитать новые координаты.
Чтобы показать, как это работает, давайте сделаем HTML-страницу, которая нарисует нам вращающийся кубик. Мы прокомментировали каждую строку кода, чтобы вы тоже смогли понять, что там происходит. Это настоящее 3D, для которого тоже нужна школьная тригонометрия :-)
Сохраните себе этот код как HTML-документ и откройте в браузере, чтобы посмотреть на вращение кубика. Если не знаете, как это сделать, — вот подробный гайд в помощь:
Спасательный круг для тех, кто начинает писать на JavaScript
<!DOCTYPE html>
<html>
<head>
<title>3D-кубик</title>
</head>
<body>
<!-- пусть кубик вращается по центру страницы-->
<div align="center">
<!-- готовим область для рисования — 200 на 200 пикселей -->
<canvas id="cubeCanvas" width="200" height="200"></canvas>
</div>
<!-- скрипт, который нарисует нам кубик -->
<script type="text/javascript">
// весь скрипт — одна большая функция
(function () {
// переменная, через которую будем работать с областью для рисования
var canvas = document.getElementById("cubeCanvas");
// размер кубика — это минимальное значение высоты или ширины холста
var size = Math.min (canvas.width,canvas.height);
// холст для рисования — двухмерный
var g = canvas.getContext("2d");
// массив с координатами вершин кубика по осям X, Y и Z
var nodes =
[[-1, -1, -1], [-1, -1, 1], [-1, 1, -1], [-1, 1, 1],
[1, -1, -1], [1, -1, 1], [1, 1, -1], [1, 1, 1]];
// а эта переменная отвечает за грани — какие вершины нужно соединить между собой по номерам, чтобы в итоге получился кубик. [0,1] означает, что будет линия между нулевой и первой вершиной, [1,3] — линия между первой и третьей вершиной и так далее
var edges =
[[0, 1], [1, 3], [3, 2], [2, 0], [4, 5], [5, 7], [7, 6],
[6, 4], [0, 4], [1, 5], [2, 6], [3, 7]];
// если нужно сделать кубик больше или меньше — используем функцию масштабирования
function scale (factor0, factor1, factor2) {
// берём каждую грань
nodes.forEach(function (node) {
// и умножаем каждую её координату на размер масштаба
node[0] *= factor0; node[1] *= factor1; node[2] *= factor2;
});
}
// вращаем кубик и получаем новые координаты для каждой вершины, а в функцию передаём углы вращения по осям X и Y
function rotateCuboid (angleX, angleY) {
// запоминаем значения синусов и косинусов для каждого угла вращения
var sinX = Math.sin(angleX);
var cosX = Math.cos(angleX);
var sinY = Math.sin(angleY);
var cosY = Math.cos(angleY);
// для каждой вершины — пересчитываем координаты после поворота
nodes.forEach(function (node) {
// помещаем значения координат вершины в отдельные переменные
var x = node[0]; var y = node[1]; var z = node[2];
// а вот тут происходит сама магия вращения — мы с помощью синусов и косинусов получаем новые координаты для каждой вершины куба
node[0] = x * cosX - z * sinX;
node[2] = z * cosX + x * sinX;
z = node[2];
node[1] = y * cosY - z * sinY;
node[2] = z * cosY + y * sinY;
});
}
// эта функция отрисовывает кубик по текущим координатам вершин
function drawCuboid () {
// берём двухмерный холст, который мы заводили раньше
g.save();
// очищаем его
g.clearRect(0, 0, canvas.width, canvas.height);
// помещаем наш будущий кубик в центр координат
g.translate(canvas.width / 2, canvas.height / 2);
// рисовать будем чёрным
g.strokeStyle = "#000000";
// начинаем рисовать по линиям
g.beginPath();
// берём каждую грань
edges.forEach(function (edge) {
// запоминаем координаты, которые нужно отрисовать
var p1 = nodes[edge[0]];
var p2 = nodes[edge[1]];
// идём на начальную точку
g.moveTo(p1[0], p1[1]);
// и виртуально соединяем её линией со второй точкой и так делаем для каждой грани
g.lineTo(p2[0], p2[1]);
});
// нарисовали — выключаем режим рисования линий
g.closePath();
// отрисовываем полностью сразу весь кубик, который у нас получился с помощью виртуальных линий
g.stroke();
// восстанавливаем холст до начального состояния — убираем с него всё, чтобы подготовиться к рисованию следующего кадра
g.restore();
}
// выбираем масштаб — уменьшим кубик в 4 раза
scale (size/4, size/4, size/4);
// здесь задаём начальные углы наклона кубика по осям X и Y. Попробуйте их поменять и посмотреть, что получится
rotateCuboid (Math.PI / 3, Math.atan(Math.sqrt(10)));
// основной цикл, который отвечает за анимацию вращения
setInterval( function() {
// поворачиваем наш кубик на выбранные углы
rotateCuboid (0.02, 0.02);
// отрисовываем кубик
drawCuboid ();
// интервал между кадрами — 10 миллисекунд
}, 10);
// закончилась главная функция
})();
</script>
</body>
</html>
Что дальше
Попробуйте поменять параметры в скрипте — масштаб, скорость вращения или углы наклона. А ещё можно попробовать сделать каждую грань своего цвета или вообще залить их сплошным цветом, чтобы эффект 3D был сильнее.
