Итак, на Реддите как-то появилась интересная задача, захотелось разобрать. Попробуйте сначала решить её сами, а если не получится — загляните в разбор, там интересно.
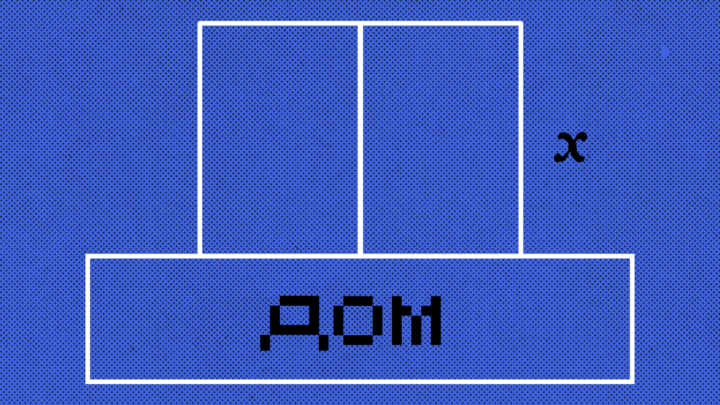
Какой-то чувак решил огородить два одинаковых прямоугольных участка у себя за домом по каким-то своим причинам. Всего у него есть 300 метров забора, которые он может поставить к дому. Одна из сторон равна иксу (подробности на картинке). А вот вопросы:
- Какая площадь участков, если взять икс (боковую сторону) за основу?
- Какая может быть максимальная площадь этих участков и какого размера должны быть границы?
Если что, забор, который надо поставить, нарисован зелёным:
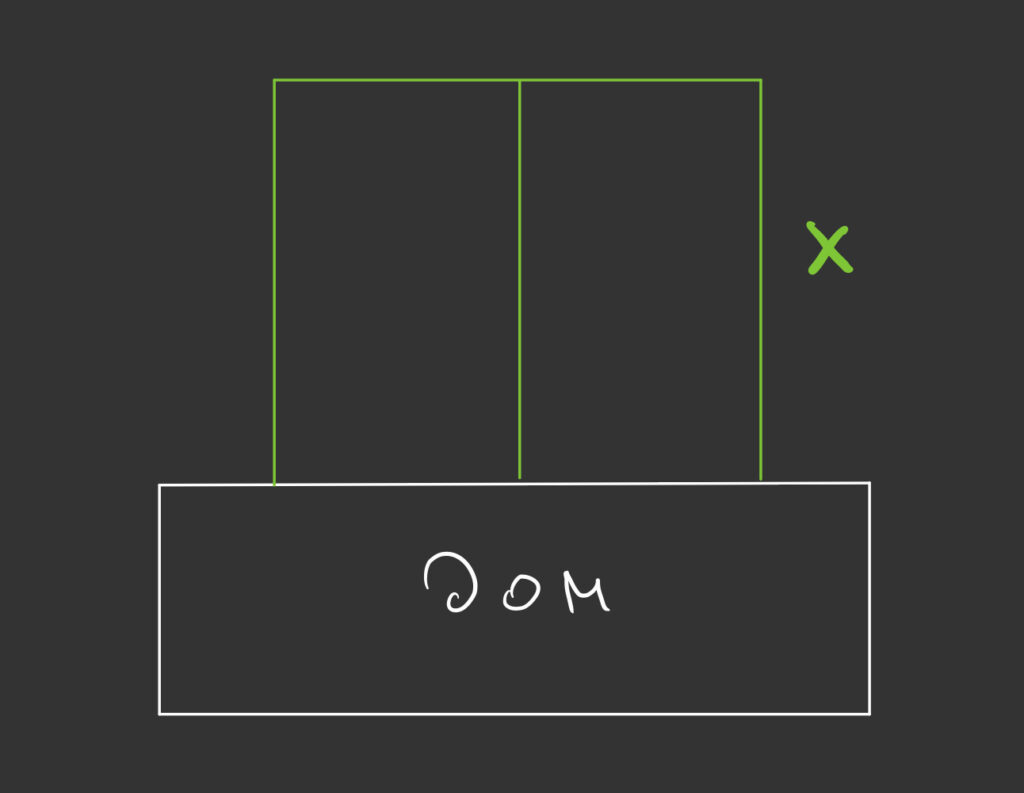
Если боковая сторона новых участков равна Х, то и две параллельных ей стороны тоже равны Х каждая, потому что по условию участки прямоугольные и одинаковые.
Получается, что верхняя сторона будет иметь длину 300 − 3Х, потому что всего у чувака 300 метров забора, а нижняя сторона примыкает прямо к дому.
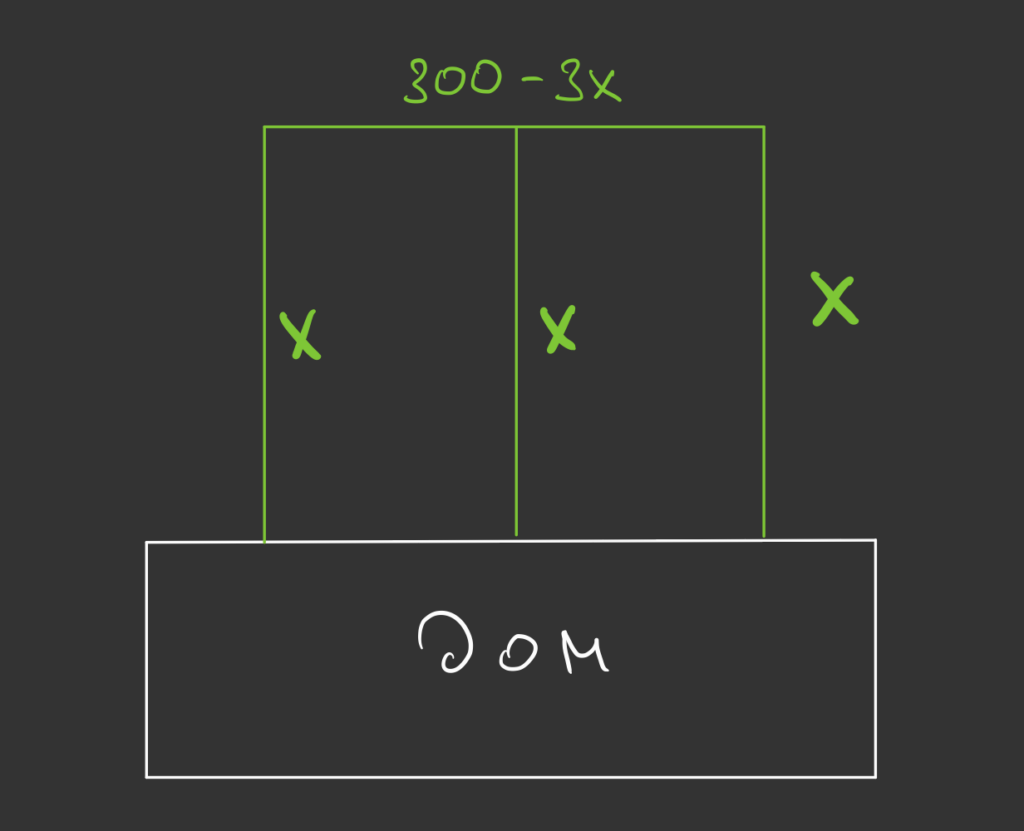
Это значит, что общая площадь участков будет равна:
Х × (300 − 3Х) = 300Х − 3Х²
Всё, мы нашли ответ на первый вопрос. Дальше попробуйте сами, а если не получится — читайте дальше.
На первом шаге мы выяснили, что общая площадь участков будет равна:
Х × (300 − 3Х) = 300Х − 3Х²
Теперь нам нужно найти, при каких значениях Х эта площадь будет максимальна. Это можно сделать двумя способами — через решение квадратного уравнения (или чуть другой математикой) или графически. Второе проще и нагляднее, а первое попробуйте всё же найти сами.
Для решения нарисуем график функции Y = 300Х − 3Х²:
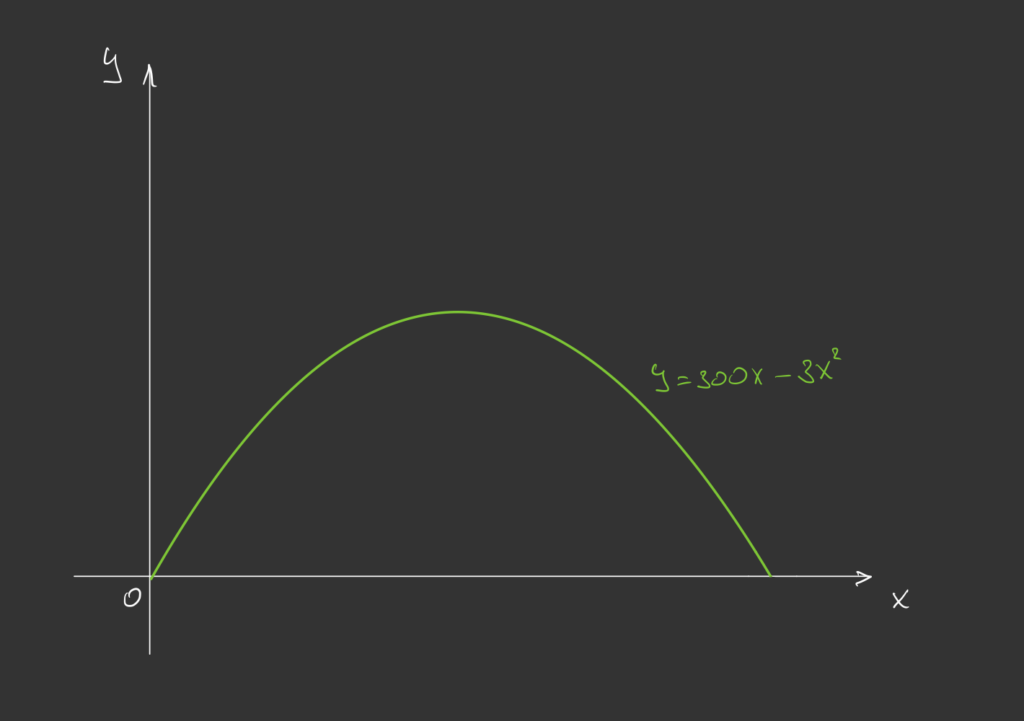
Перед нами — параболическая функция (потому что квадратное уравнение). Особенность параболы в том, что её график симметричен относительно точки перегиба — там, где функция меняет направление. Это значит, что если нам нужно найти максимальную площадь (а это у нас максимальное значение Y по графику), нам нужно найти значение Х в точке перегиба, то есть на вершине параболы.
Парабола пересекает ось Х в двух точках — это значит, что при этих значениях Х игрек равен нулю. Найдём эти точки:
если Х × (300 − 3Х) = 0 → Х = 0 или (300 − 3Х) → Х = 100
Мы нашли точки пересечения с осью Х — это 0 и 100. Так как парабола симметрична, то вершина параболы будет находиться ровно посередине между этими точками — то есть на отметке в 50:
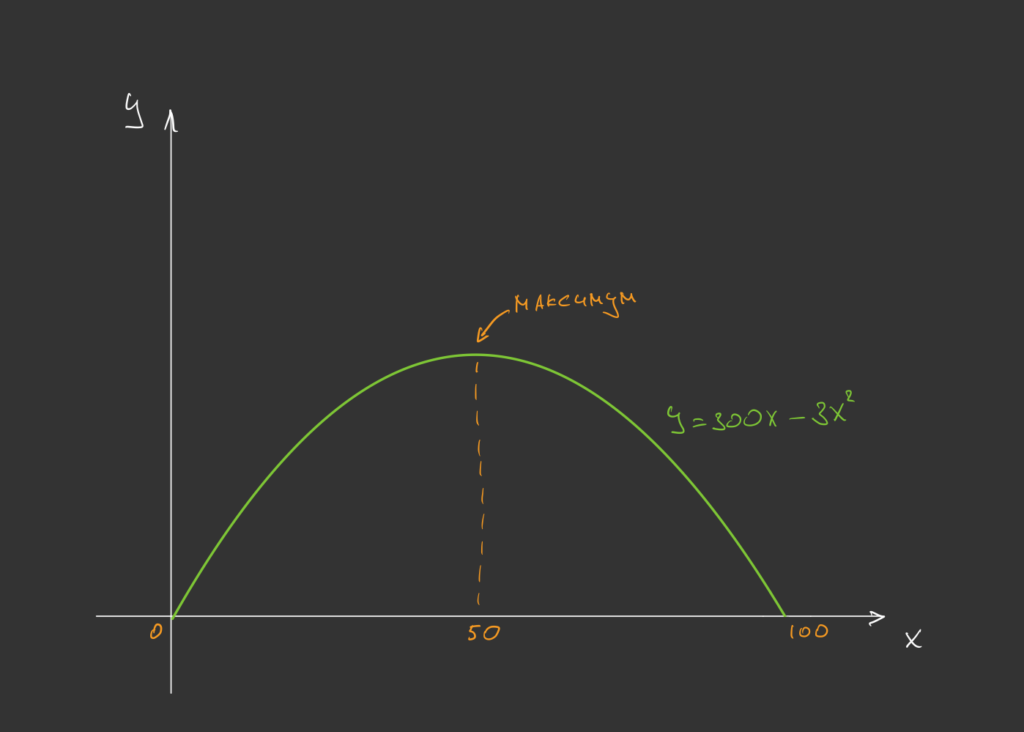
Получается, что максимальная площадь, огороженная таким забором, равна:
50 × (300 − 3 × 50) = 50 × 150 = 7 500 м²
А размеры заборов простые: три по 50 метров и один на 150 метров.
Вот мы нашли ответ и на второй вопрос. Если справились сами — красавчики.
 Хитрая задача про реку от русского преподавателя в американском колледже
Хитрая задача про реку от русского преподавателя в американском колледже Что не так с челленджем из Тиктока на скорость сбора бутылок: разбираем как математики
Что не так с челленджем из Тиктока на скорость сбора бутылок: разбираем как математики Что не так с задачей про степени, которую нужно РЕШИТЬ УСТНО, и как она всё-таки решается
Что не так с задачей про степени, которую нужно РЕШИТЬ УСТНО, и как она всё-таки решается Задача про золото для тех, кто нестандартно мыслит
Задача про золото для тех, кто нестандартно мыслит Интересная задача про велосипеды, которую можно решить намного быстрее, чем кажется
Интересная задача про велосипеды, которую можно решить намного быстрее, чем кажется Безумная задача про среднюю скорость, которую все решают неправильно
Безумная задача про среднюю скорость, которую все решают неправильноВам слово
Приходите к нам в соцсети поделиться своим мнением о задаче и почитать, что пишут другие. А ещё там выходит дополнительный контент, которого нет на сайте: шпаргалки, опросы и разная дурка. В общем, вот тележка, вот ВК — велком!