Среди части пользователей Ютуба и Тиктока вирусится видео, где два парня на скорость собирают бутылки в ящик. Правила простые:
- В один ряд стоят 24 бутылки и пустой ящик для них. Ими занимается первый игрок.
- Другой ряд — такой же, из бутылок и ящика. Это для второго игрока.
- По команде игроки начинают одновременно брать по одной бутылке, ставить в ящик и переходить к следующей.
- Но у игроков разная стратегия. Первый начинает с ближней к ящику бутылки и постепенно двигается к дальним, а второй наоборот — начинает с дальних и заканчивает ближними.
❓ Внимание, вопрос: чья стратегия выигрышнее?
В жизни это выглядит так:
Во всех челленджах (и в исходном видео) побеждает второй игрок — тот, который начинает сбор с дальних бутылок и заканчивает теми, которые стоят возле ящика. НО ПОЧЕМУ ЭТА СТРАТЕГИЯ ВЫИГРЫШНАЯ? Нет ли здесь какого-то подвоха? Что про это думает математика и логика?
Давайте разбираться. Но сначала разберёмся с кое-чем другим.
Почему это стало виральным?
Смотрите, в сети есть куча роликов с посылом «Думай иначе и получи более крутой результат в тех же условиях». Сюжеты разные, но общий смысл такой: главный герой применяет смекалку и выходит победителем из ситуации.
Когда мы смотрим такие ролики, то кажется, что этот подход можно применить вообще в любой ситуации, главное — научиться такому стилю мышления. Но это только на картинке всё так красиво, а в жизни всё это может сработать совсем иначе. В соцсетях важны просмотры и лайки, и если для этого можно немного что-то скорректировать, чтобы круто смотрелось, — почему бы и нет?
Что думает математика про это видео
С точки зрения математики, логики и здравого смысла всё просто: оба игрока при равенстве всех остальных факторов закончат одинаково.
Теперь разберём всё сухо и беспристрастно.
Для простоты возьмём 6 бутылок с расстоянием в метр между каждой (и тем же расстоянием между ящиком и первой бутылкой). Дальше вы увидите, что, независимо от количества бутылок, вычисления будут такими же.
Разберём стратегию первого игрока
Первый игрок начинает с ближайших бутылок. Это значит, что он сначала переместится к первой, возьмёт её, переместится к ящику и положит её туда. Так как между всеми элементами у нас 1 метр, то общее расстояние на этом этапе будет 1 + 1 = 2 метра:
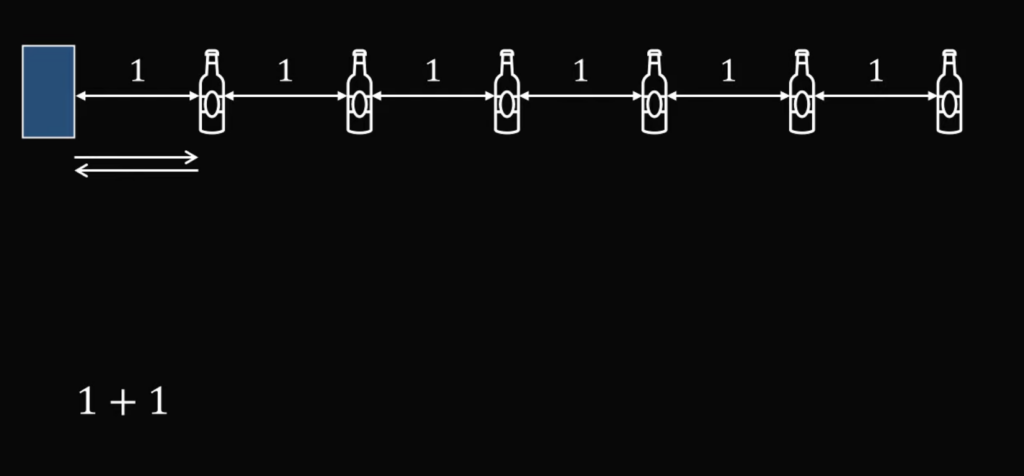
Дальше двигаемся по той же стратегии и считаем расстояние:
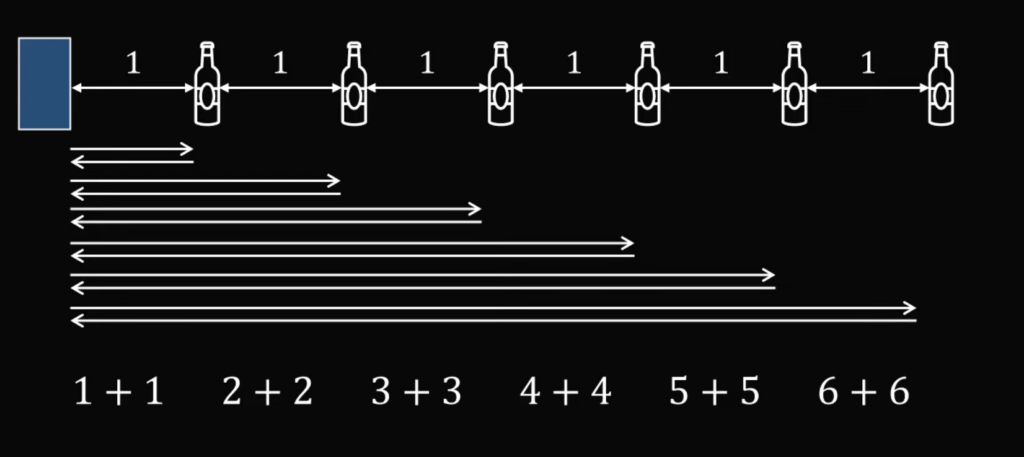
Получается, что общее расстояние, которое пройдёт первый игрок, будет равно:
1 + 1 + 2 + 2 + 3 + 3 + 4 + 4 + 5 + 5 + 6 + 6 →
2 × (1 + 2 + 3 + 4 + 5 + 6) = 2 × ([6 × 7] / 2) = 6 × 7 = 42
Это значит, что суммарно первый игрок пройдёт 42 метра, чтобы собрать все бутылки.
Разберём стратегию второго игрока
Второй игрок начинает с самых дальних бутылок и движется к ближним. На первом этапе ему нужно дойти до дальней, взять её, отнести к ящику и положить её туда.
Для этого ему нужно пройти 6 + 6 = 12 метров:
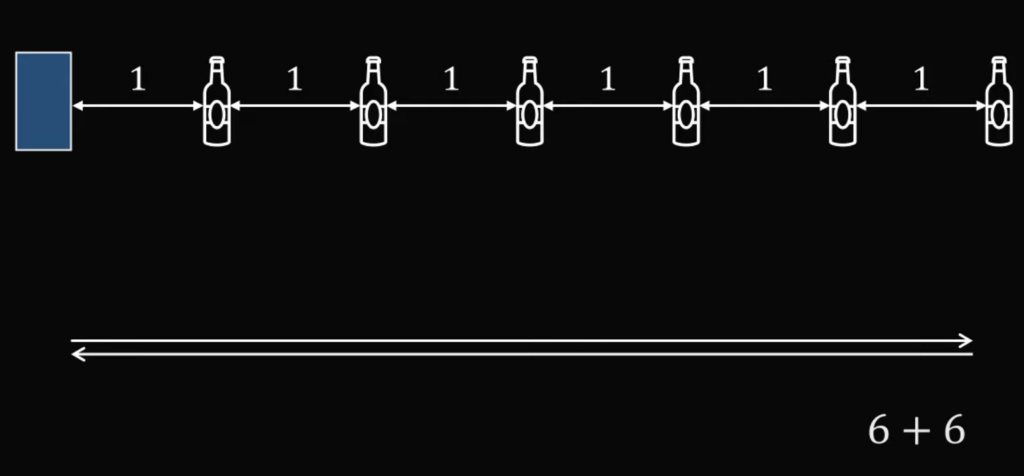
Так шаг за шагом он доберётся до первой бутылки:
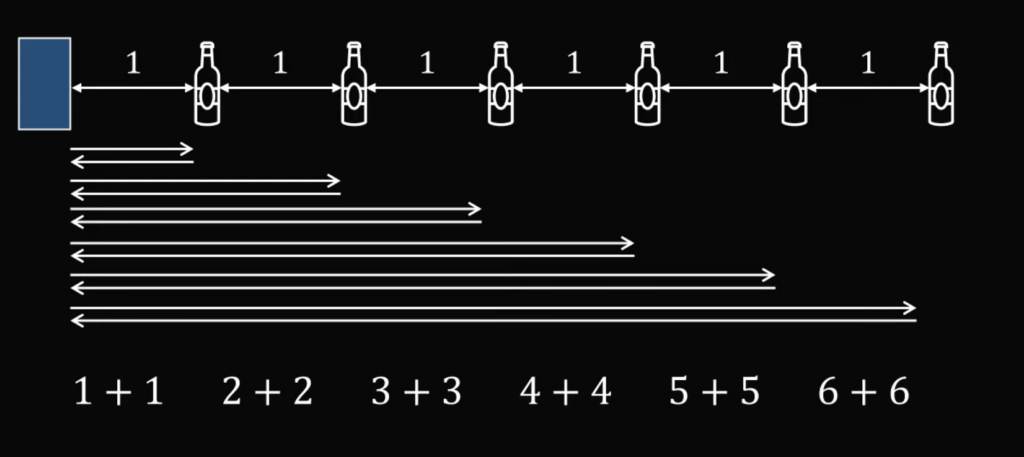
Но если мы посмотрим на цифры, то увидим, что второй игрок пройдёт то же расстояние, что и первый:
2 × (1 + 2 + 3 + 4 + 5 + 6) = 2 × ([6 × 7] / 2) = 6 × 7 = 42
Получается, что оба игрока пройдут одно и то же расстояние, а при равной скорости им на это потребуется одно и то же время (потому что скорость одинаковая). А если скорость не равна, то конкурс на выбор подхода не имеет смысла, потому что тут решает не метод сбора, а ловкость и быстрота ног.
Более того, даже если к ним присоединится третий игрок, который будет брать бутылки вообще в случайном порядке, то закончит их собирать вместе с первыми двумя. Потому что математика.
Хитрая задача про реку от русского преподавателя в американском колледже
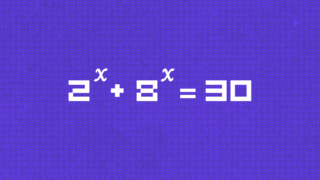Что не так с задачей про степени, которую нужно РЕШИТЬ УСТНО, и как она всё-таки решается
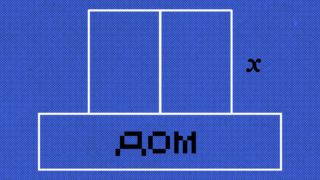Необычная задача с Реддита про чувака и периметр забора
Задача про золото для тех, кто нестандартно мыслит
Интересная задача про велосипеды, которую можно решить намного быстрее, чем кажется
Безумная задача про среднюю скорость, которую все решают неправильноИ что всё это значит?
То, что ко всему в интернете (да и вокруг нас в целом) нужно относиться критически. Если что-то становится популярным и там используется какой-то нестандартный подход — это необязательно правда. Да, там будет тысяча просмотров, но к реальности это не будет иметь никакого отношения.
В нашем примере есть много вариантов, почему могла победить вторая стратегия:
- авторы специально заранее продумали такие съёмки, чтобы создать драматургию;
- второй игрок тупо быстрее;
- расстояние между бутылками было неодинаковое;
- и ещё может быть десяток других причин.
Вывод такой: если вы видите, где два одинаковых с точки зрения математики подхода показывают разные результаты, это не крутой лайфхак — это человеческий фактор :)
Вам слово
Приходите к нам в соцсети поделиться своим мнением о разборе и почитать, что пишут другие. А ещё там выходит дополнительный контент, которого нет на сайте: шпаргалки, опросы и разная дурка. В общем, вот тележка, вот ВК — велком!
